Exploding and Collapsing Boxes
REPORT
Suppose you have a bunch of 10:1 machines that collapse dots put inside their box. These machines will collapse 10 dots at a time, but each time they do that, they put 1 dot into the next box to the left. For example, start with a box that has two-hundred and thirty four dots in it.

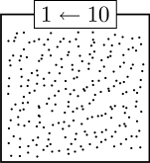
Then, after all machines have collapsed all that they can, the boxes will have the following dot pattern:
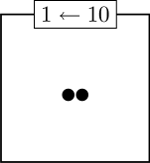
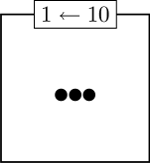
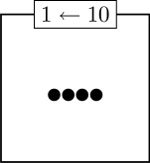
What will happen if instead we have 1:2 machines with 3 dots in the first box? How about 4:2 machines with 19 dots in the first? What about 3:2 machines?
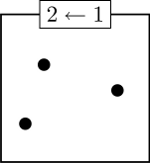
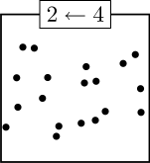
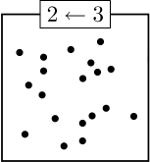
For each different type of machine, what is the fewest number of dots needed initially in the first box that will require five boxes after all of the dots have been collapsed?
Our exploration was inspired by the Global Math Project Exploding Dots activity.

