
Do You Want to Know a Secret? – Activity Directions
Students explore function rules and linear relationships through input and output tables and tile patterns.
Activities on this page:
Secret Calculators
Part I - Directions:
Numbers were entered into calculators. Study the input/output table to find
the secret and figure out what was done to the number put in the calculator
(the input) to get the number that came out of the calculator (the output).
First, write the secret in words. Then write an equation, using x for input
and y for output, that represents the secret.
Example:
| Input (x) | Output (y) |
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
| 4 | 5 |
|
| the secret in words: |
| add 1 to an input number to make an output number |
|
| the secret in symols |
| x + 1 = y |
|
Problems:
| 1. |
| Input (x) | Output (y) |
| 1 | 5 |
| 2 | 6 |
| 3 | 7 |
| 4 | 8 |
|
|
|
| 2. |
| Input (x) | Output (y) |
| 1 | -2 |
| 2 | -1 |
| 3 | 0 |
| 4 | 1 |
|
|
|
| 3. |
| Input (x) | Output (y) |
| 1 | 5 |
| 2 | 10 |
| 3 | 15 |
| 4 | 20 |
|
|
|
| 4. |
| Input (x) | Output (y) |
| 1 | -2 |
| 2 | -4 |
| 3 | -6 |
| 4 | -8 |
|
|
|
| 5. |
| Input (x) | Output (y) |
| 1 | 7 |
| 2 | 10 |
| 3 | 13 |
| 4 | 16 |
|
|
|
| 6. |
| Input (x) | Output (y) |
| 1 | -1 |
| 2 | 1 |
| 3 | 3 |
| 4 | 5 |
|
|
|
| 7. |
| Input (x) | Output (y) |
| 1 | 2 |
| 2 | -2 |
| 3 | -6 |
| 4 | -10 |
|
|
|
Part II - Directions:
Numbers were entered into calculators. Someone has told you the secret!
Read the given secret and interpret it into an input/output table by first
choosing an input and then writing its output. Next, write an equation,
using x for input and y for output, that represents the secret.
Problems:
| 1. |
|
| the secret in words: |
| add 7 to an input number to make an output number |
|
|
| 2. |
|
| the secret in words: |
| subtract 5 from an input number to make an output number |
|
|
| 3. |
|
| the secret in words: |
| multiply input number by -1 to make an output number |
|
|
| 4. |
|
| the secret in words: |
| multiply an input number by 3 then add 8 to make an output number |
|
|
| 5. |
|
| the secret in words: |
| multiply an input number by 4 then subtract 11 to make an output number |
|
|
| 6. |
|
| the secret in words: |
| add 2 to an input number then multiply the result by -3 to make an output number |
|
|
| 7. |
|
| the secret in words: |
| subtract 6 from an input number then divide the result by 3 to make an output number |
|
|
Part III - Directions:
Make your own secret! First, write down your secret in words. Then, make an
input/output table by choosing at least 4 input numbers and writing their
output number. Next, write an equation, using x as the input number and y
as the output number, that represents your secret. Finally, challenge your
friends to find your secret! Let them choose their input numbers and you
give them the correct output numbers for each input. Can your friends
figure out your secret?
Tile Patterns
Materials:
- graph paper
- colored pencils
- colored square tiles (at least 2 colors)(optional)
Directions:
For each of the pattern series, complete the following steps and answer the
questions.
- Draw the given first 3 patterns on graph paper. (If you are using tiles, build each pattern using only one color of tile.)
- On the same graph paper, follow the pattern and draw the 4th and 5th patterns in the series. (If you are using tiles, build patterns 4 and 5 using only one color of tile.)
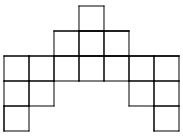
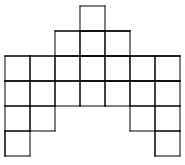
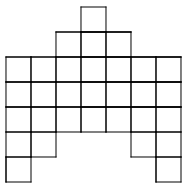
- How is the pattern changing? How will the ninth pattern look?
- How would you explain to someone how to build any pattern number?
- What part of the pattern is constant? Choose a color to shade the squares that are constant. (If you are building the patterns with tiles, use one color of tile for the constant squares.)
- What part of the pattern is changing or variable? Choose a color to shade the squares that are variable. (You may choose to use 5 colors to shade the new squares in each pattern of the series
- Write a rule using algebraic notation to describe how to build any pattern in the series. Let n represent the number of the pattern and let a represent the amount of tiles. Test your rule with the patterns you have drawn.
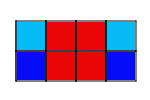
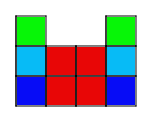
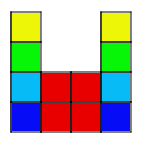
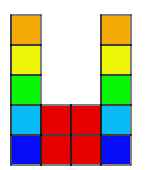
Example:
Problem:
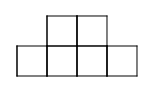 |
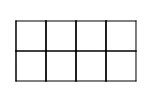 |
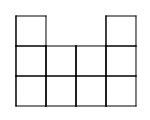 |
|
|
| Pattern 1 |
Pattern 2 |
Pattern 3 |
Pattern 4 |
Pattern 5 |
Solution:
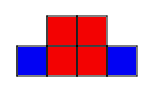 |
 |
 |
 |
 |
| Pattern 1 |
Pattern 2 |
Pattern 3 |
Pattern 4 |
Pattern 5 |
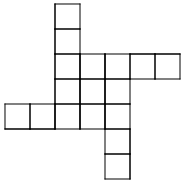
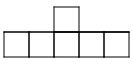
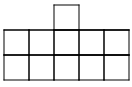
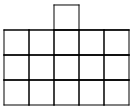
3. The outside columns are growing, while the middle two columns
stay the same. The ninth pattern will look like 9 squares in each column on
the outside and 4 squares in the middle.
4. Start by building a bigger square with four small squares. Then,
starting at the bottom of the bigger square, build a column of squares as
tall as the pattern number on each side of the bigger square.
5. The four squares in the middle are constant.
6. The columns on the sides are variable.
7. 4+2n=a
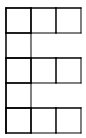
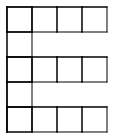
Problems:
-
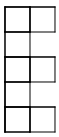 |
 |
 |
|
|
| Pattern 1 |
Pattern 2 |
Pattern 3 |
Pattern 4 |
Pattern 5 |
-
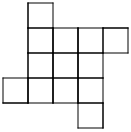 |
 |
 |
|
|
| Pattern 1 |
Pattern 2 |
Pattern 3 |
Pattern 4 |
Pattern 5 |
-
 |
 |
 |
|
|
| Pattern 1 |
Pattern 2 |
Pattern 3 |
Pattern 4 |
Pattern 5 |
-
 |
 |
 |
|
|
| Pattern 1 |
Pattern 2 |
Pattern 3 |
Pattern 4 |
Pattern 5 |





















